小学二年级奥数教程第17讲:有趣的余数除法

小学二年级奥数教程第17讲:有趣的余数除法

小学二年级奥数教程第17讲:有趣的余数除法
在除法中，当被除数除以除数(除数不等于0)出现了余数(余数要比除数小)，就称为有余数的除法．

   在有余数的除法中，我们知道：

    (1)被除数=除数×商+余数；

    (2)除数=(被除数一余数)÷商．

    在解题时，我们常常要注意到：余数一定比除数小；在除法算式中，余数个数的多少、余数的大小是随着祓除数和除数的不同而不同的．

例1、下面的算式是一个有余数的除法，问：被除数最大是几?最小是几?    ，

口÷8= 9……口

解 从算式中可知，除数是8，商是9，根据余数比除数小，余数只能是1，2，…，7，再根据“被除数=除数×商+余数”，所以，被除数最大是

             8×9+7=79

被除数最小是：8×9+1=73

  随堂练习1  下面的有余数的除法算式中，被除数最大是几?最小是几?    ，

  (1) 口÷7=8……口；

  (2) □÷10=9……□．

例2、 下面的算式是一个有余数的除法，要使除数最小，被除数是儿?

       口÷口=1 8……28．

    解  因为除数比余数大，而余数是28，所以除数最小是29，于是，被除数是

29×18 +28=550．

   随堂练习2  下面的算式是一个有余数的除法，要使除数最小，被除数是几?

           口÷口=8……18．

例3、 写出所有除以5所得的商和余数相同的数．

    解 除数是5，余数要比除数小，因此余数只能为1，2，3，4，再根据“被除数=除数×商+余数”来求出被除数．

    5×1+1=6， 5×2 +2=12，

    5×3+3=18．5×4+4=24．

所以符合要求的数为6，12，18，24．

例4、 节日里街上挂起彩灯，从第一盏灯开始，按照红、黄、蓝、绿各一盏的顺序依次重复排下去．问：

    (1)第50盏灯是什么颜色?

    (2)这50盏灯里红灯有几盏?

解  因为彩灯的排列顺序为红、黄、蓝、绿各一盏依次重复排下去，也就是说把4盏灯作为一个周期，所以根据这一规律可先算出50盏灯里有几个周期：

50÷4=12……2

    (1)以上算式表示50盏灯共有12个周期，余2表示多2盏灯，即从下一个周期起，从红灯开始数起的第二盏灯为黄灯，所以第50盏灯的颜色是黄颜色；

(2)因为每个周期里有l盏红灯，这50盏灯里共有12个周期，就有12盏红灯，再加上多出来的2盏灯里有l盏灯是红灯，所以这50盏灯里红灯一共有13盏．

说明 许多事物的变化都是有周期性的，掌握事物变化的周期，就能灵活运用周期变化规律解决实际问题．在用有余数的除法去解决周期性问题时，把握两个关键：

(1)要明确以几个数为一个周期；

(2)余数是表示为新一轮周期开始的第几个数，如余数为3，则表示新一轮周期开始后的第3个数．

   随堂练习3 根据下面图形的规律推算出第16个图形是什么?

    (1)口△△口△△口△△口△△…

(2)☆○○△☆○○△☆○○△…

例5、 2007年的6月1日儿童节是星期五，那么，39天后是星期几?

解 一个星期是7天，“六一”儿童节是星期五，以这天为这周的开始，后面几天分别为星期六、星期日、星期一、星期二、星期三和星期四，将这样的7天作为一组，39天里有39÷7=5(组)……4(天)，这4天是第三个星期的前四天，分别是星期五、星期六、星期日、星期一．所以39天后是星期一．

   随堂练习4  2007年1月1日是星期一，那么小明这年生日2月28日是星期几?

例6、 有一列数：2，3，5；2，3，5；2，3，5；…．问：

    (1)第26个数是几?

    (2)这26个数的和是几?

    解  (1)从这列数中可以看出，2，3，5为一组，因此26个数可以组成

    26÷3=8(组)……2(个)，

所以，第26个数为3．

    (2)要求这26个数的和，可以先求出一组3个数的和，如2+3+5=10，26个数中有这样的8组再加上第9组的前2个数2和3，所以26个数的和为

       10×8+2+3=85．

随堂练习5 有一列数：2，4，1；2，4，1；2，4，1；…．问：第25个数是几?这25个数的和是多少?

例7、 三个字母“A、B、C”和六个文字“数学奥林匹克”分别依次循环出现，一个字母和一个文字对应一组，见下表：

(1)第51组、第89组分别是什么?

(2)用(A，林)表示1000年，那么2004年对应哪一组?

    解如果按上面组合的方法一个个地排列出来，显然很费时．考虑到每组都是由一个字母和一个文字组成的．而且字母是每3个为一组，文字是每6个为一组，因此可以用除法运算的余数来求解．

    (1)因为51÷3=17，51÷6=8……3，所以第51组字母为C，文字为奥；

    89÷3=29……2，89÷6=14……5，所以第89组字母为B，文字为匹．

    (2)用(A，林)表示1000年，那么1002年对应的是(C，克)，2004年比1002年多1002年，1002÷3=334，1002÷6=167，余数都为0，所以对应的也应是(C，克)．

练  习  题

1、填空

(1) □÷7=6……3，□=（     ）；

(2)51÷△=6……3，△=(      )；

(3)18÷☆=☆……2，☆= (    )；

(4)◇÷△=4……5，△最小是(  )，◇是(    )；

(5)○÷8=3……□，□最大是(  )，○是(  )；    。

(6)口÷4= ◎……◎，◎可以分别是(    )，对应的口分别是(    )．

2、明明到少年宫看演出，他坐在第8排，如果用他的座位号除以排号，商和余数正好是2，明明坐在8排几座?

3、跨植树节那天，同学们按1棵松树、2棵香樟树、3棵广玉兰的顺序栽树，第15棵是什么树?第30棵又是什么树?

4、国庆节挂彩灯，按“红、黄、兰、白、绿、紫”的顺序挂，一共挂了50只彩灯．问：第50只彩灯是什么颜色的? 红色的彩灯共有多少只?

5、2004年的5月1日是星期六，那么那年的国庆节是星期几?

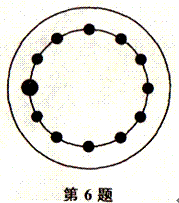
6、如图，有11个小黑点1个大黑点，如果从某个小黑点按顺时针方向数到200时，正好是大黑点，请指出是从哪个小黑点开始的?

7、在下表中，上排的数字按1～9周期变化，中排的数字按1～6周期变化，下排的数字按1～4周期变化，将每列的上、中、下三个数字组成一个数组，如第l组为(1，1，1)，第8组为(8，2，4)，那么第2008组是什么?