小学二年级奥数教程第29讲:简单的操作问题
在某些数学问题中,需要一边做、一边探索、一边调整,这样的问题将思考和“操作”结合在一起,我们称为“操作题”.解决这类问题要综合运用我们所学的知识和技巧.在二年级结束的时候,我们来思考一些这类问题.
例1、在一个5×5的方格棋盘上,每个格内都有一盏灯和一个按钮,按钮每按一次,与它同一行和一列的方格中的灯泡都改变一次状态,即由亮变成不亮或不亮变成亮.如果开始时,每盏灯都是不亮的,请说明,怎样按法,才能使全部灯变亮? ’
解 因为按单数次按钮,可以使灯改变状态,我们将第一列的5个按钮全按一次,全部灯就变亮了.这是因为,经过如上按动后,除第一列外,其余格上的每个灯都只改变一次状态(由不亮变亮),而第一列中的每格,都改变了5次状态,5是单数,所以,第一列的每盎灯也全变亮了.想一想,还有其他的按法吗?
随堂练习1 有7只杯子放在桌上,杯口全部朝上,每次翻动其中的3只,最少翻动几次,能使杯子全部杯口朝下.
例2、如图30—1,10枚棋子围成一个圆圈,依顺时针方向编上号码1,2, 3,…,8,9,10.然后,按顺时针方向,每隔一枚拿走一枚,直到剩下一枚棋子为止.如果剩下的这枚棋子的号码是6,那么第一枚被取走的棋子的号码是几?
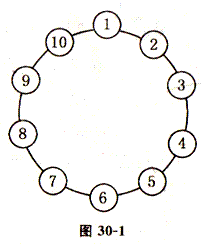
解我们先作一个试验,随意选一个起点开始拿,例如第1个拿1号,按隔1个取一个的方法依次拿走1,3,5,7,9,2,6,10,8,最后剩下的棋子是4号(如图30—2).(划斜线表示起始点,格子表示最后剩下的)
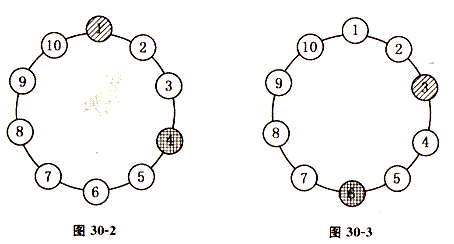
由于6号在4号的前面第2个,因此,我们只需将试验时的起点1向前移2个,即移到第3号.于是,如果第1枚棋子取3号,那么,以后依次取走5,7,9,1,4,8,2,10,最后剩下6(如图30—3).(划斜线表示起始点,格子表示最后剩下的)
随堂练习2 如果上题按逆时针方向,每隔一枚拿走一枚,直到最后剩下一枚棋子的号码是8,那么第一枚被取走的棋子的号码是几?
例3、如图30—4,四个小动物换座位,开始时,小鼠坐在1号位,小猴坐在2号位,小兔坐在3号位,小猫坐在4号位.以后,它们不停地交换位置,第一次上下两排交换,第二次是在第一次交换后再左右两排交换,第三次再上下两排交换,第四次再左右两排交换……这样一直交换下去.问:第十次交换位置后,小兔坐在第几号位置上?
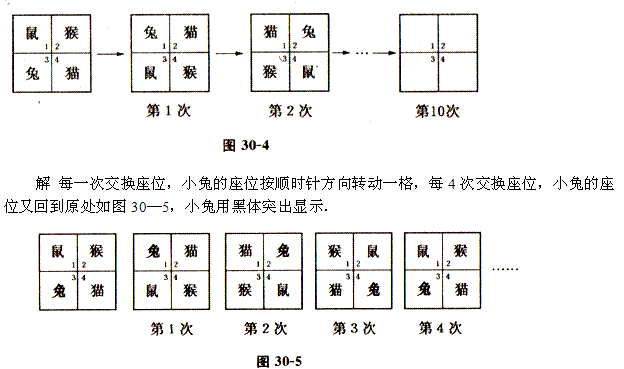
经过8次交换位置后,小兔又回到原处(3号位),第9次相当于第1次的位置;第10次相当于第二次的位置,此时,小兔在2号位置.
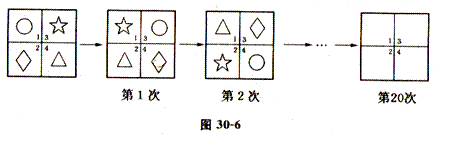
随堂练习3如图30一6,小胖在田字格内放了☆、◇、○和△四个图形,并且编了位置的号码.小胖第一次把左右两列图形交换,第二次再把上下两行图形交换,第三次再把左右两列图形交换……这样一直交换下去.问:第二十次交换后,☆在第几号格子中?
例4、 9张卡片,上面分别写着1~9这9个自然数.能不能将这9张卡片平均分成3组,使每组中3张卡片上数的和相等.
解 能,由于1+2+3+4+5+6+7+8+9=45=15+15+15.因此,所分的三组中,3个数的和均应等于15.
下面就是一种分法:
第1组:(1,9,5)
第2组:(3,4,8)
第3组:(2,6,7)
还可以有其他分法,小朋友不妨试一试.
随堂练习4 有9张卡片上分别写着4~12这9个自然数,将这9张卡片平均分成三组,使每组中3张卡片上数的和相等.
例5、如图30—7是用6个小圆片组成的尖头向上的图形,请移动2个小圆片,使图形变成尖头向下的图形吗?
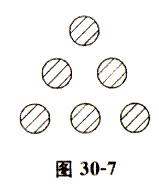
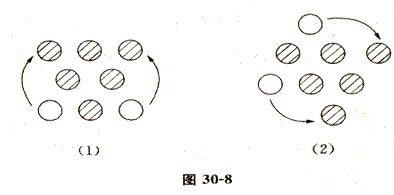
解 因为只能移动2个圆片,那么应该有4个圆片是不需要移动的.如图(1),可以把图下方3个圆片中的边上2个圆片移到上方,或者如图(2),把最上方的圆片移到中间一排右边,把下方3个圆片中左边一个移到最下方.
随堂练习5 如图30—9是用6个圆片组成的尖头向左的图形,现在要移动2个圆片,使它变成尖头向右的图形,怎么移?
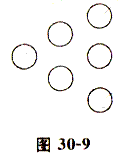
例6、有一大杯水,还有两只分别为3毫升和5毫升的量杯,怎样才能准确地倒出4毫升的水呢?
解 如果5毫升的量杯中有1毫升水,那么再把3毫升量杯装满后倒入5毫升的量杯中,这时杯中正好是4毫升水.
倒的具体步骤如下:
第一次把3毫升量杯装满水后倒入5毫升量杯;第二次再把3毫升量杯装满倒入5毫升量杯中,此时3毫升杯中余1毫升水;第三次把5毫升杯内的水倒掉,将3毫升杯内余下的l毫升水倒入5毫升杯子,最后再装满3毫升的水倒入5毫升的杯子,这时5毫升杯内就有4毫升水.
随堂练习6 一只大瓶装有10 kg油,现在有可盛7 kg油和3 kg油的空瓶各1只,怎样利用这三只瓶子能倒出5 kg油?
例7、有8个玻璃球,颜色、大小都一样.但其中有1个玻璃球比其他球都重.你能利用天平秤只称两次就找到这个球吗? 、
解 解决这个问题,要充分利用天平,可以量出两边弹子球重量是否相等.如果两边平衡,就表明要找的玻璃球不在其中.
第一次,天平两边各任意放3个球,这时会有两种可能,可能之一是两边平衡,那么稍重的玻璃球在余下的2个球中,因此第二次只要称余下的2个球,哪一边重就能确定要找的玻璃球在哪一边.可能之二是天平的一边比另一边重,那么较重一边的3个球中一定有这个玻璃球.第二次称时只要从这3个球中任意取2个,如果平衡,剩下的那个球就是;如果不平衡,较重的一边就是要找的玻璃球.
随堂练习7 有8块石头,外形、颜色都一模一样,其中有一块重量比较轻.现在有一个天平,最少称几次才能找到这块石头?

















