小学二年级奥数教程第27讲:智力计数
小学二年级奥数教程第27讲:智力计数
计数,就是数数,这是最简单的算术问题.但是,最简单的问题常常是最重要的问题。随着问题性质和条件的日益多样化,计数成了发展我们智慧很重要的领域,成为数学中的一个有趣而又深奥的领域.我们从小学点计数的简单技巧,就会使我们头脑逐步灵活,为今后学习和生活打下良好的基础.
计数之所以可以培养聪明的头脑,最主要原因就是,它要求我们善于变换角度看问题,善于细心抓问题本质,善于从实践中发现规律.
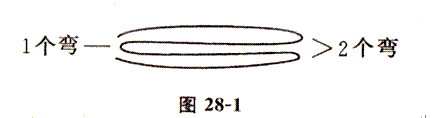
例1、 将一根绳子对折2次,然后每隔一定长度剪1刀,共剪了4刀.请问:原来的绳子被剪成几段?
解绳子折2次后,折成相等的4份,剪4刀后,剪出5份,每份有4段,照理说,应该有4+4+4+4+4 = 20(段).
但由于在对折两次后,在对折后的绳子两头共有3个弯(如图28—1),它们连在一起,只能算一段,因此,实际上共有20—3 = 17(段).
随堂练习1 将一根绳子对折后再对折,然后每隔一定长度剪1刀,一共剪3刀.那么原来的绳子被剪成了几段?
例2、 一张纸片,第1次将它撕成4片,以后每次在撕过的纸片中取一片,再将它撕成4片.这样撕5次后,一共有多少张纸片?
解 我们只要注意一下,每撕一片,纸片增加了多少张就可以了.由于每次我们只将原有纸片中的一片撕成4片,其他的纸片没有撕,所以每撕一次,(除第一次)纸片数增加了4—1 = 3(片).这样,撕5次后,纸片总数为4+3+3+3+3 = 16(片).
随堂练习2 一张彩纸,第一次将它剪成4片,以后每次在剪过的纸片中取一片,再将它剪成4片,这样剪10次后,一共有多少张纸片?
例3、 小明从一层楼走到四层楼,每走一层要花2分钟,小明要花多少分钟才能走到四层楼?
解画图28—2分析:
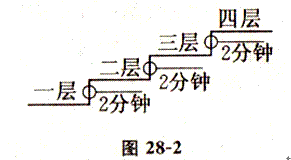
从一层楼走到四层楼共经过三层楼梯,每走一层楼梯(即从一层楼到二层楼,或从二层楼到三层楼……)需要2分钟,现在共走三层楼梯需要2+2+2 = 6(分钟).
随堂练习3 亮亮的家住在七楼,亮亮走一层楼要用2分钟,亮亮从一楼走到七楼要用多少分钟?
例4、 (1)如图,给出四个平面图形,数一数每个平面图各有多少个顶点?多少条边?它们分别围成了多少个区域(即将每个图形分成几部分)?请将结果填入下表:
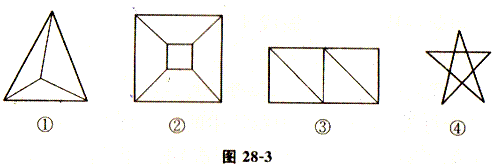
顶点数 | 边数 | 区域数 | |
图① | |||
图② | |||
图③ | |||
图④ |
(2)分析表上的每一行所填的三个数,猜一猜平面图形的顶点数、边数、区域数之间有什么关系.(请列出一个式子)
(3)现已知某一个平面图形有44个顶点,45个区域,试根据(2)所列出的式子确定这个图形的边数.
解 (1)见下表:
顶点数 | 边数 | 区域数 | |
图① | 4 | 6 | 3 |
图② | 8 | 12 | 5 |
图③ | 6 | 9 | 4 |
图④ | 10 | 15 | 6 |
(2)我们发现以下规律:
边数 顶点数+区域数
图① 6 4+3 =7
图② 12 8+5 = 13
图③ 9 6+4 =1 0
图④ 15 10+6 = 16
规律是:6 = 7—1,12 = 13—1,9 = 10—1,15 = 16—1。
边数=顶点数+区域数一1. (公式)
(3)现已知顶点数= 44,区域数= 45.
根据(2)总结的规律(公式),所以,
边数= 44+45—1 = 88.
答:边数是88.

















