随堂练习2 小学二年级奥数教程第27讲:智力计数
例5、 将一个圆形纸片用直线划分成若干部分,请问:用5条直线最多可将圆形纸片划分成多少部分?
解 很显然,一条直线将圆形纸片划分成2部分;两条直线,最多将圆形纸片划分成4部分.现在考虑三条直线最多将圆形纸片划分成几部分,我们用图形来说明问题,如图28—4早三条直线将图划分的各种情况:,
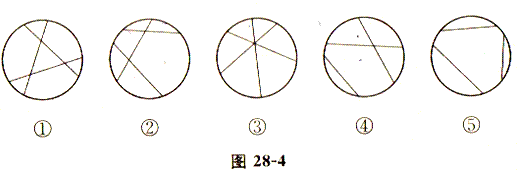
由上面5个图形可见,图①分出的部分最多,由此可知,若希望将纸片划分成尽可能多的块数,应该使新划出的直线与原有的直线在圆内都相交,而且交点各不相同,这时增加部分的数目等于此时圆内的直线数.依此规律,直线的条数与圆内划分出部分的最多块数有以下规律: ’
直线条数 纸片最多划分成的部分数
1 1+l
2 1+1+2
3 1+1+2+3
4 1+1+2+3+4
5 1+1+2+3+4+5
所以,5条直线最多可将圆形纸片划分成
1+1+2+3+4+5 = 16(块).
随堂练习4 用8条直线最多可将一张正方形纸片划分成多少部分?
在计数时,我们还可以把解决问题的方法先分类,然后数出每一类方法的数量,最后把它们相加,能得到总数,这也是一种科学、周密的思考方法,能保证数出的结果不重复也不遗漏.下面就举些例子来熟悉这个方法.
例6、 小明、小华和小强去公园游玩,他们三人站在一排,请一位游人给他们三人合影,他们想多照几张,每两张之间三人排的次序都不同,他们一共应照几张照片?
解 可以将三人的位置分为左、中、右,用图28—5简单表示.
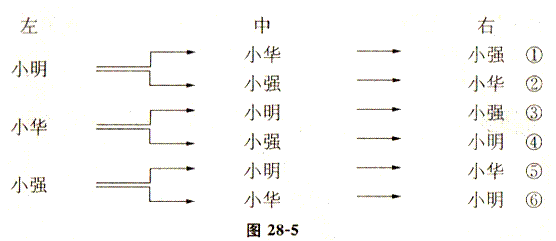
再简明表示为(小明、小华、小强),(小明、小强、小华),(小华、小强、小明),(小华、小明、小强),(小强、小明、小华),(小强、小华、小明)共6种排法.
随堂练习5 把○、☆、◇兰个图形排成一行,一共有多少种不同的排法?
例7、 有8张卡片,上面分别写着1到8,从中取出3张,要使这3张卡片上的数字和为9,有多少种不同的取法?
解“取3张卡片使上面的数字和为9”,我们将它分三步:取第一张,取第二张,取第三张,首先确定3张卡片中数字最大的卡片.
显然,8和7都不能取.因为最小的两张卡片1和2与它们相加都超过9,所以从6开始取.
第1张取6,6+1+2=9,另两张分别取1和2.
第l张取5,5+1+3=9,另两张分别取1和3.
第1张取4,4+2+3=9,另两张分别取2和3.
而最大数字不超过3的三张卡片加起来和都小于9.所以只有3种不同的取法.
随堂练习6 有9张卡片,上面分别写着1到9,从中取出3张,要使这3张卡片上的数字和为11,有多少种不同的取法?
例8、 用数字1,2,3,4可以组成多少个没有重复数字的两位数?
解一个两位数由十位数和个位数组成,只要这两位数上的数字排定了:这个两位数就确定了.分两步完成:第一步先排十位数,第二步排个位数.共有4个数字可用,具体排法
如下:
(1)十位数排1有12,13,14共三种;
(2)十位数排2有21,23,24共三种;
(3)十位数排3有31,32,34共三种;
(4)十位数排4有41,42,43共三种.
合起来,一共有3+3+3+3 = 12(种).
随堂练习7 用数字0,1,6,8可以组成没有重复数字的两位数一共有几个?

















